BOSOR5 can handle segmented and branched, elastic-plastic shells of revolution with discrete ring stiffeners, meridional discontinuities, and multi-material construction. BOSOR5 also includes creep. The shell wall can be made up of as many as six layers, each of which is a different nonlinear (elastic-plastic) material. In the pre-buckling analysis large-deflection axisymmetric behavior is presumed. Bifurcation buckling loads are computed corresponding to axisymmetric or non-axisymmetric buckling modes.
The strategy for solving the nonlinear pre-buckling problem is such that the user obtains reasonably accurate answers even if he or she uses very large load or time steps. This strategy is based on a sub-incremental iteration method in which the size of the sub-increment is automatically determined so that the change in stress is less than a certain prescribed percentage of the effective stress at each material point in the shell wall. Discrete rings of arbitrary cross section are considered to be assemblages of thin rectangular elements.
The input is interactive, as with BOSOR4 (BIGBOSOR4). BOSOR5 has been checked by means of numerous runs in which the results have been compared to other analyses and to tests. BOSOR5 does not supersede BOSOR4 or BIGBOSOR4 because it has no modal vibration capability, nor can it handle non-axisymmetrically loaded shells.
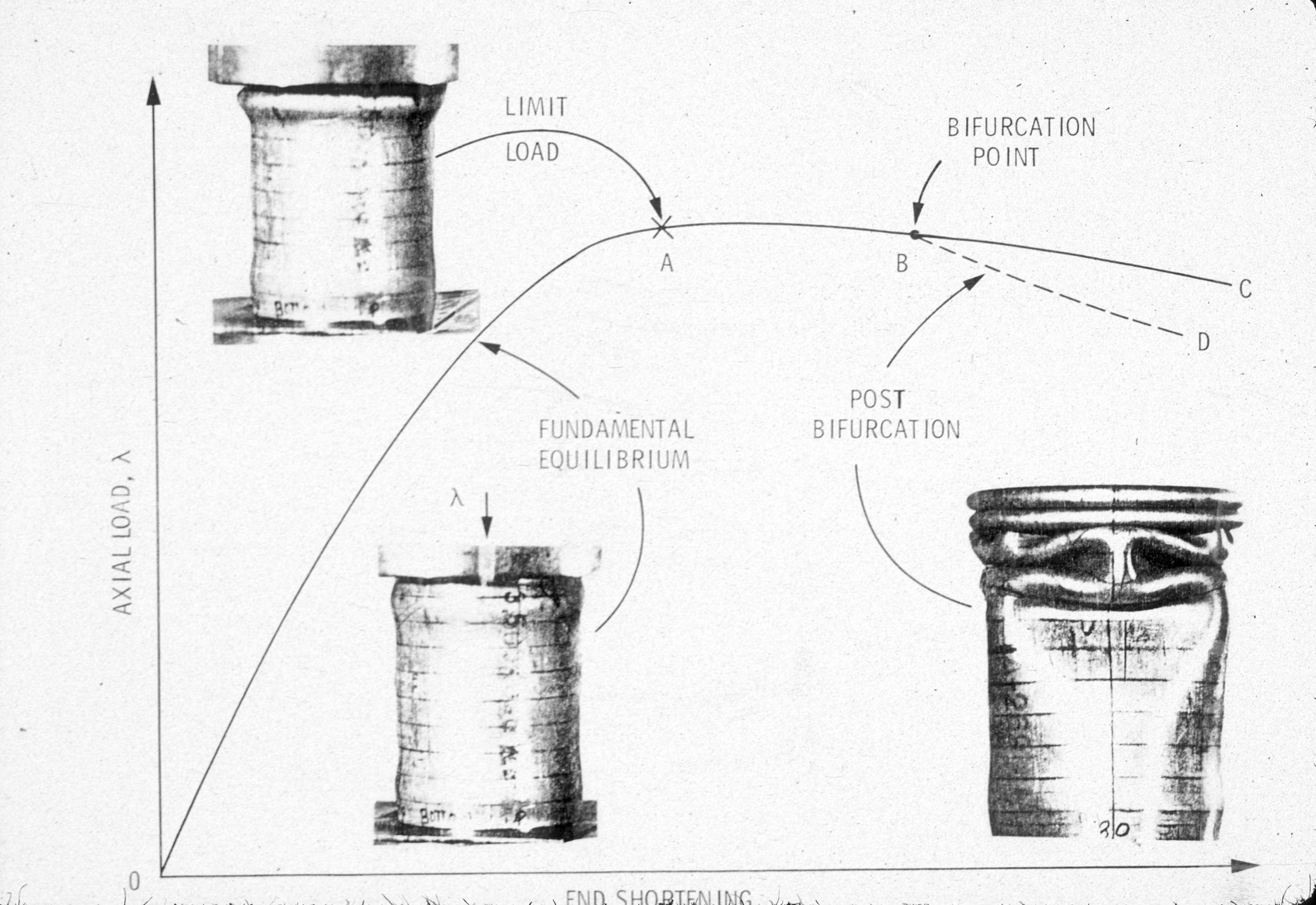
Graphic from Pressure Vessels and Piping: Design Technology – 1982, A Decade of Progress, S.Y. Zamrik and D. Dietrich, editors, published by ASME; Chapter 2.4 “Plastic Buckling” by David Bushnell, pp. 47-117.
Load-end-shortening curve with limit point A, bifurcation point B, and post-bifurcation equilibrium path, BD.
For a gallery of the kind of problem that can be solved by BOSOR5, see the slide show. This slide show is primarily composed of pictures taken from the long, illustrated abstracts of papers about BOSOR5 and results generated from executions of BOSOR5.
NOTE: BOSOR5 does NOT supersede BOSOR4 or BIGBOSOR4. BOSOR4/BIGBOSOR4 is restricted to the study of shells made of material that is linear elastic. BOSOR5 is more restricted than BOSOR4/BIGBOSOR4 in the type of analysis that BOSOR5 can do, but BOSOR5 will handle elastic-plastic material and creep.
Abstracts and Papers
-
Bifurcation Buckling Of Shells of Revolution Including Large Deflections, Plasticity and Creep, David Bushnell, Lockheed Palo Alto Research Laboratory, 3251 Hanover Street, Palo Alto, California 94304 USA. International Journal of Solids and Structures, Vol. 10, pp. 1287-1305, 1974.
Left: Elastic-plastic aluminum cone-cylinder combination tested under uniform external pressure by G.D. Galletly at the University of Liverpool. Right: Discretization for processing by BOSOR5. Plastic flow is confined to the small region in the neighborhood of the corner between the cone and the cylinder.
A summary is first presented of the conceptual difficulties and paradoxes surrounding plastic bifurcation buckling analysis. Briefly discussed are non-conservativeness, loading rate during buckling, and the discrepancy of buckling predictions with use of J2 flow theory vs J2 deformation theory. The axisymmetric pre-buckling analysis, including large deflections, elastic-plastic material behavior and creep is summarized. Details are given on the analysis of non-symmetric bifurcation from the deformed axisymmetric state. Both J2 flow theory and J2 deformation theory are described. The treatment, based on the finite-difference energy method, applies to layered segmented and branched shells of arbitrary meridional shape composed of a number of different elastic-plastic materials. Numerical results generated with a computer program based on the analysis are presented for an externally pressurized cylinder with conical heads.
-
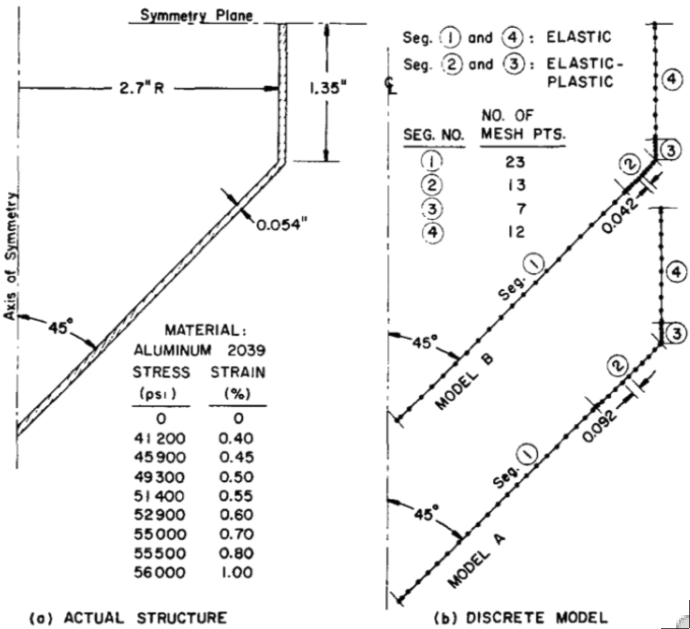
Comparisons Of Test and Theory for Nonsymmetric Elastic-Plastic Buckling of Shells of Revolution, David Bushnell, Lockheed Palo Alto Research Laboratory, 3251 Hanover Street, Palo Alto, California 94304 USA. Gerard D. Galletly, Dept. of Mechanical Engineering, The University, Liverpool L69-3BX, England. International Journal Solids Structures, Vol. 10, pp. 1271-1286, 1974.
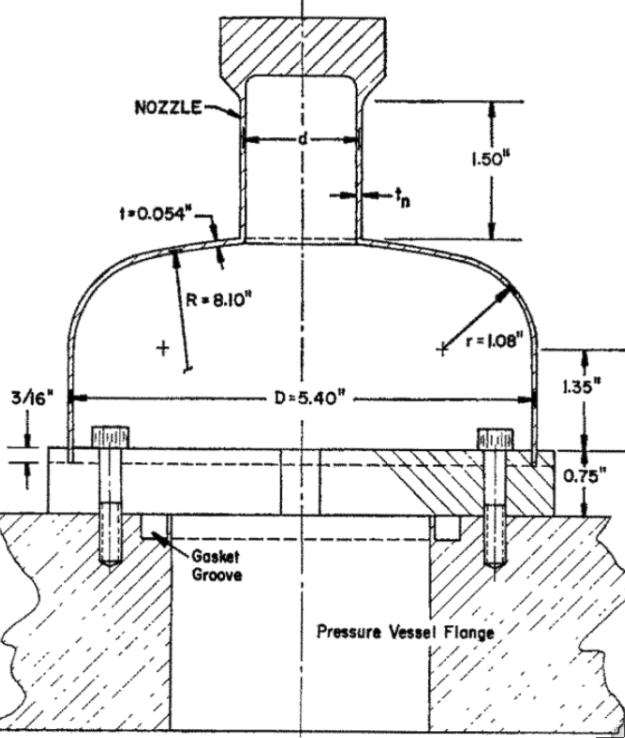
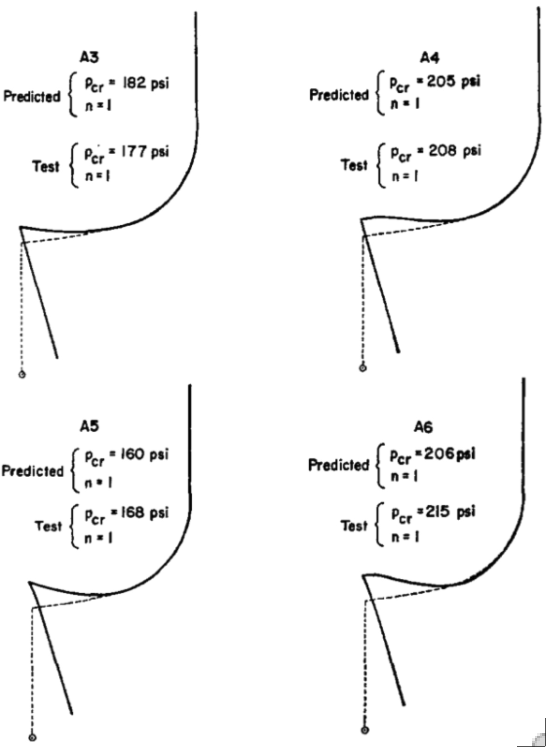
Left: Elastic-plastic aluminum nozzle-torispherical shell combination tested under uniform external pressure by G.D. Galletly at the University of Liverpool. Right: Critical elastic-plastic buckling modes predicted by BOSOR5 for four different specimens: A3, A4, A5, A6. In all four cases the critical buckling mode has n = 1 circumferential wave, which corresponds to tilting of the nozzle.
Experimental and analytical buckling pressures are presented for very carefully fabricated thin cylindrical shells with 45, 60 and 75° conical heads and for cylindrical shells with torispherical heads pierced by axisymmetric cylindrical nozzles of various thicknesses and diameters. Non-symmetric buckling occurs at pressures for which some of the material is loading plastically in the neighborhoods of stress concentrations caused by meridional slope discontinuities. The buckling pressures for the cone-cylinder vessels are predicted within 2.6 per cent and for the pierced torispherical vessels within 4.4 per cent with use of BOSOR5, a computer program based on the finite difference energy method in which axisymmetric large deflections, nonlinear material properties and non-symmetric bifurcation buckling are accounted for. The predicted buckling pressures of the pierced torispherical specimens are rather sensitive to details of the analytical model in the neighborhood of the juncture between the nozzle and the head. The buckling pressures of the cone-cylinder vessels can be accurately predicted by treatment of the wall material as elastic, enforcement of the full compatibility conditions at the juncture in the pre-buckling analysis, and release of the rotation compatibility condition in the bifurcation (eigenvalue) analysis.
-
BOSOR5 – A Computer Program for Buckling of Elastic-Plastic Complex Shells of Revolution Including Large Deflections and Creep: Vol. 1: User’s Manual, Input Data , David Bushnell, Lockheed Palo Alto Research Laboratory, 3251 Hanover Street, Palo Alto, California 94304 USA. Lockheed Missiles & Space Company, Inc. Report LMSC-D407166, December, 1974.
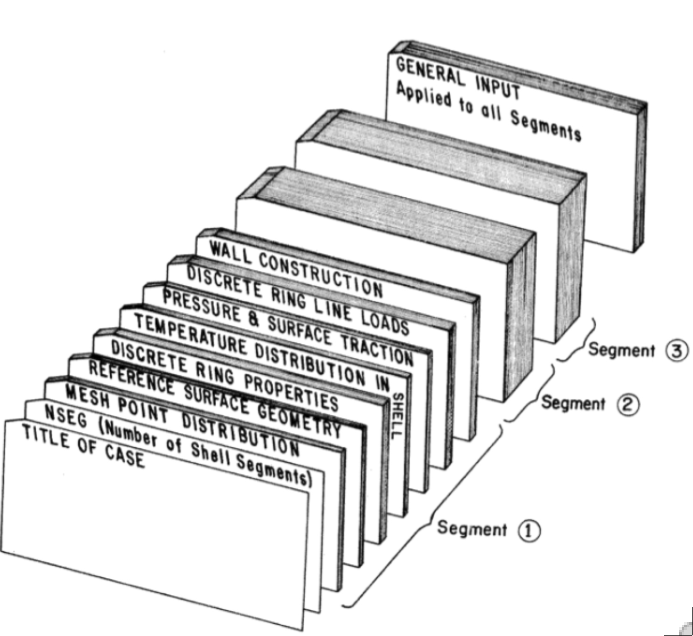
Quaint schematic of a typical input “deck” (punched cards) for BOSOR5.
This volume contains the instructions to the user for constructing data decks for the BOSOR5 computer program. BOSOR5 runs on the UNIVAC 1108 and the CDC 6600. (2011 NOTE: BOSOR5 runs on LINUX.) It is divided into three separate programs, a pre-processor, a main-processor, and a post-processor. These programs may be run as one job in a run stream or separately. The program includes a restart capability. BOSOR5 can handle segmented and branched shells with discrete ring stiffeners, meridional discontinuities, and multi-material construction. The shell wall can be made up of as many as six layers, each of which is of a different nonlinear material. In the pre-buckling analysis axisymmetric behavior is presumed. Bifurcation buckling loads are computed corresponding to axisymmetric or non-axisymmetric buckling modes. The strategy for solving the nonlinear pre-buckling problem is such that the user obtains reasonably accurate answers even if he or she uses very large load or time steps. BOSOR5 has been checked by means of numerous runs in which the results have been compared to other analyses and to tests.
-
BOSOR5 – A Program for Buckling of Elastic-Plastic Complex Shells of Revolution Including Large Deflections And Creep, David Bushnell, Lockheed Palo Alto Research Laboratory, 3251 Hanover Street, Palo Alto, California 94304 USA. Computers & Structures, Vol. 6, pp. 221-239. 1976.
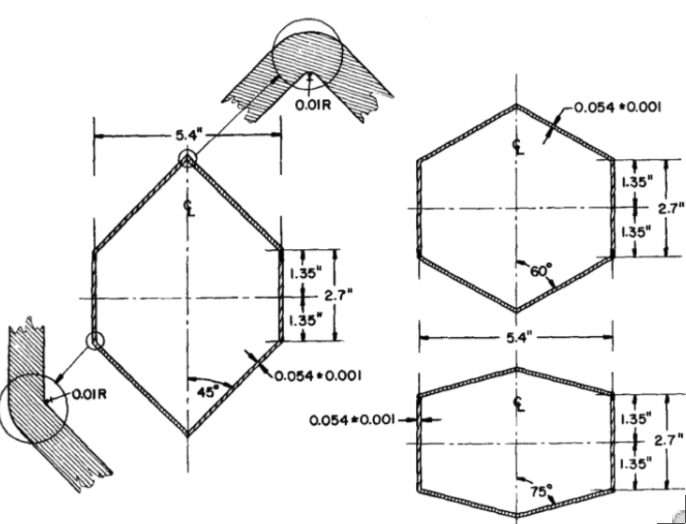
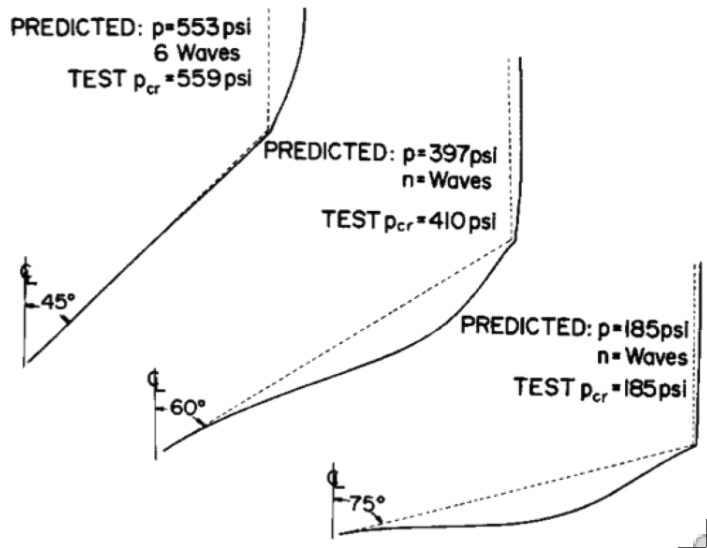
Left: Three elastic-plastic aluminum cone-cylinder combination tested under uniform external pressure by G.D. Galletly at the University of Liverpool. Right: Critical elastic-plastic buckling modes and pressures from test and BOSOR5 theory.
BOSOR5 can handle segmented and branched shells with discrete ring stiffeners, meridional discontinuities, and multi-material construction. The shell wall can be made up of as many as six layers, each of which is a different nonlinear material. In the pre-buckling analysis large-deflection axisymmetric behavior is presumed. Bifurcation buckling loads are computed corresponding to axisymmetric or non-axisymmetric buckling modes. The strategy for solving the nonlinear pre-buckling problem is such that the user obtains reasonably accurate answers even if he uses very large load or time steps. BOSOR5 has been checked by means of numerous runs in which the results have been compared to other analyses and to tests.
-
Buckling of Elastic-Plastic Shells of Revolution with Discrete Elastic-Plastic Ring Stiffeners, David Bushnell, Lockheed Palo Alto Research Laboratory, 3251 Hanover Street, Palo Alto, California 94304 USA. Int. J. Solids Structures, 1976, Vol. 12, pp. 51-66.
Model used in BOSOR5 for the representation of ring stiffeners. The shell wall and each of the segments of each ring may consist of elastic-plastic material.
The theory is summarized for axisymmetric prebuckling and nonsymmetric bifurcation buckling of ring-stiffened shells of revolution. The analysis is based on finite difference energy minimization in which moderately large meridional rotations, elastic-plastic effects, and primary or secondary creep are included. This theory is implemented in a computer program called BOSOR5, for the analysis of segmented and branched ring-stiffened shells of revolution of multi-material construction. Comparisons between test and theory are given for axisymmetric collapse and nonsymmetric bifurcation buckling of 69 machined ring-stiffened aluminum cylinders submitted to external hydrostatic pressure. Because most of the cylinders fail at an average stress that corresponds to the knee of the stress-strain curve, the analytical predictions are not very sensitive to modeling particulars such as nodal point density or boundary conditions. Agreement between test and theory is improved if the analytical model reflects the fact that the shell and rings intersect over finite axial lengths.
-
A Strategy for the Solution of Problems Involving Large Deflections, Plasticity and Creep, David Bushnell, Lockheed Palo Alto Research Laboratory, 3251 Hanover Street, Palo Alto, California 94304 USA. International Journal for Numerical Methods in Engineering, Vol. 11, 683-708, 1977.
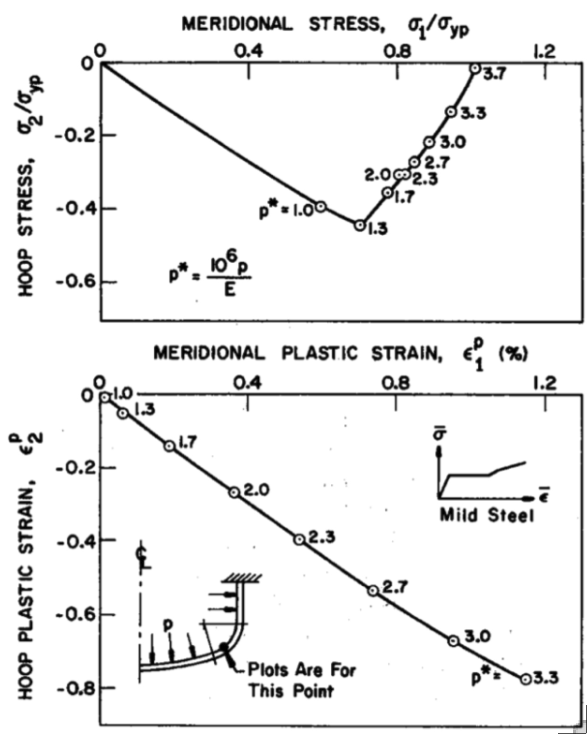
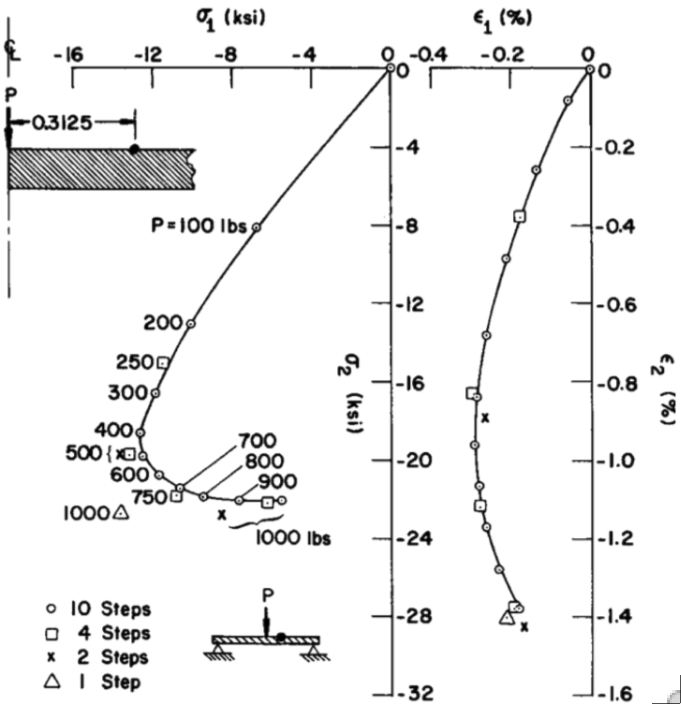
Left: Paths followed in stress space (top) and strain space (bottom) by a material point in an internally pressurized elastic-plastic torispherical vessel head made of mild steel. Center and Right: Paths followed in stress space (center) and strain space (right) by a material point in a circular flat plate with a concentrated load, P.
A strategy for solving problems involving simultaneously occurring large deflections, elastic-plastic material behavior, and primary creep is described. The incremental procedure involves a double iteration loop at each load level or time. In the inner loop the material properties are held constant and the non-linear equilibrium equations are solved by the Newton-Raphson method. These equations are formulated in terms of the tangent stiffness. In the outer loop the plastic and creep strains are determined and the tangent stiffness properties are updated with use of a sub-incremental algorithm. The magnitude of each time sub-increment is determined such that the change in effective stress is less than a preset percentage of the effective stress. The strategy is implemented in a computer program, BOSOR5, for the analysis of shells of revolution. Examples are given of elastic-plastic deformations of a centrally loaded flat plate and elastic-plastic-creep deformations of a beam in bending. The major benefits of the sub-incremental technique are the increased reliability with which problems involving non-linear plastic and time-dependent material behavior can be solved and the greatly relaxed requirement on the number of load or time increments needed for satisfactory results.
-
Plastic Buckling, David Bushnell, Lockheed Palo Alto Research Laboratory, 3251 Hanover Street, Palo Alto, California 94304 USA. Pressure Vessels and Piping: Design Technology – 1982, A Decade of Progress, S.Y. Zamrik and D. Dietrich, editors, published by ASME; Chapter 2.4, pp. 47-117. 1982.
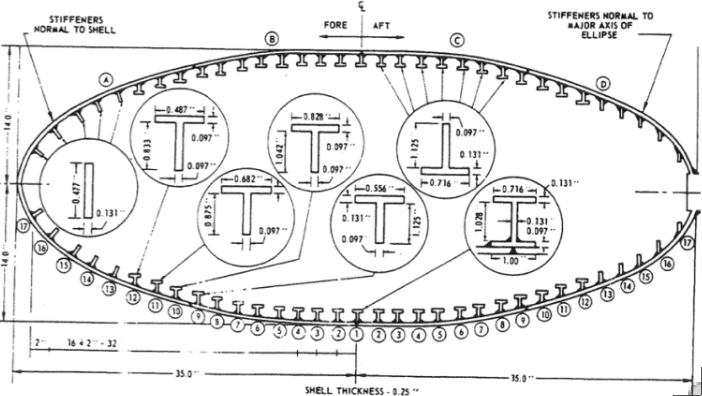
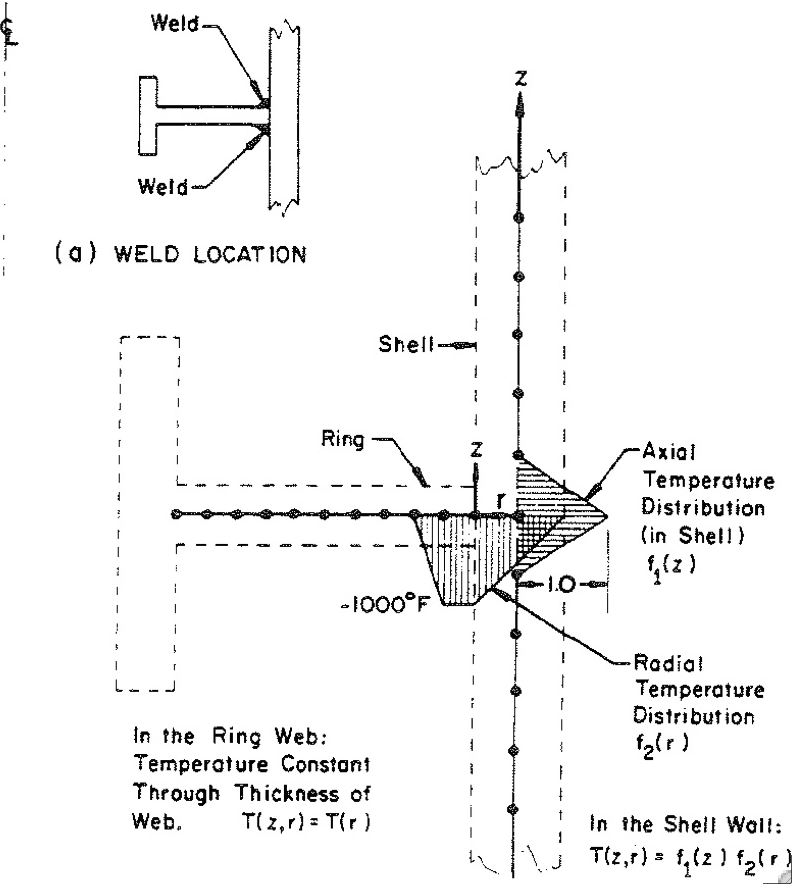
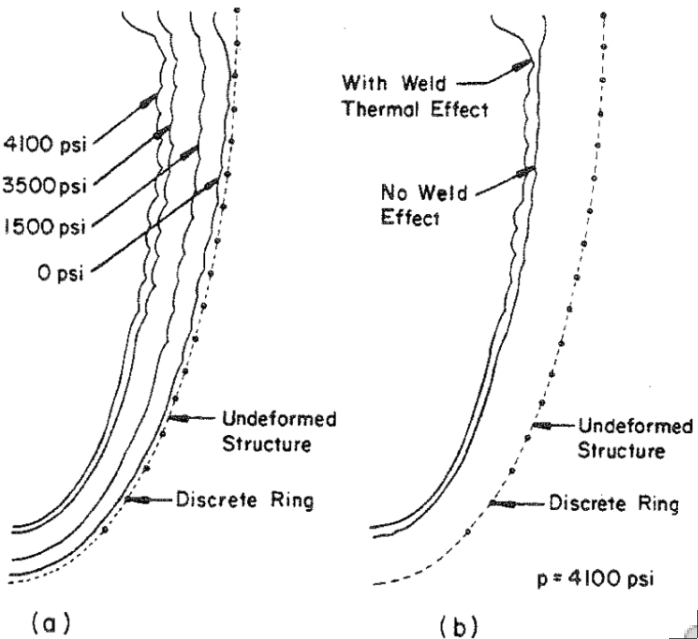
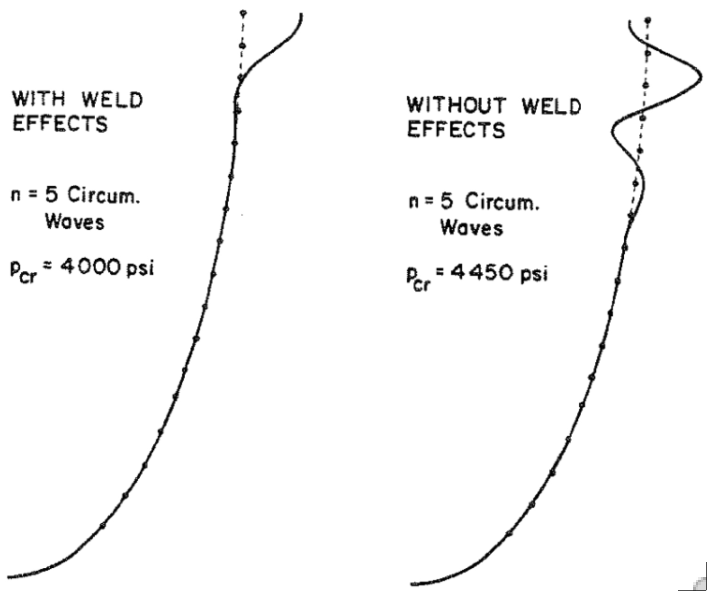
Top Left: Ring-stiffened football-shaped shell tested under uniform external pressure at the David Taylor Model Basin. The rings are welded to the shell. Top Right: The axisymmetric pre-buckling deformation caused by the welding process is simulated in BOSOR5 by local cooling down near the junction of the ring web with the shell wall. Bottom Left: Axisymmetric pre-buckling deformation under the external pressure including and neglecting the effect of welding. Bottom Right: Non-axisymmetric buckling including and neglecting the effect of welding.
The phenomenon of plastic buckling is first illustrated by the behavior of a fairly thick cylindrical shell, which under axial compression deforms at first axisymmetrically and later non-axisymmetrically. Thus, plastic buckling encompasses two modes of behavior, nonlinear collapse at the maximum point in a load versus deflection curve and bifurcation buckling.
-
Computerized Analysis of Shells-Governing Equations, David Bushnell, Lockheed Palo Alto Research Laboratory, 3251 Hanover Street, Palo Alto, California 94304 USA. Computers & Structures, Vol. 18, pp 471-536, 1984.
Schematic of what the lower left-hand part of the stiffness matrix looks like for a BOSOR5 model with two segments joined intermittently to each other.
This paper opens with a general discussion of terms in an energy function that might be the basis from which equations governing stress, stability, and vibration analyses are derived. The energy expression includes strain energy of the shell and discrete stiffeners, kinetic energy of the shell and stiffeners, constraint conditions with Lagrange multipliers, and other terms arising from the change in direction of applied loads during deformation. Brief discussions are included of the coupling effect between bending and extensional energy needed for the analysis of layered composite shells or elastic-plastic shells, nonlinear terms, and the form that the energy expression takes upon discretization of the structure.
-
BOSOR5 – Program for Buckling of Complex, Branched Shells of Revolution Including Large Deflections, Plasticity and Creep, David Bushnell, Lockheed Missiles & Space Company, Palo Alto, CA, USA. Structural Analysis Systems – Vol. 2, A. Niku-Lari, editor, Pergamon, pp. 25-54, 1986.
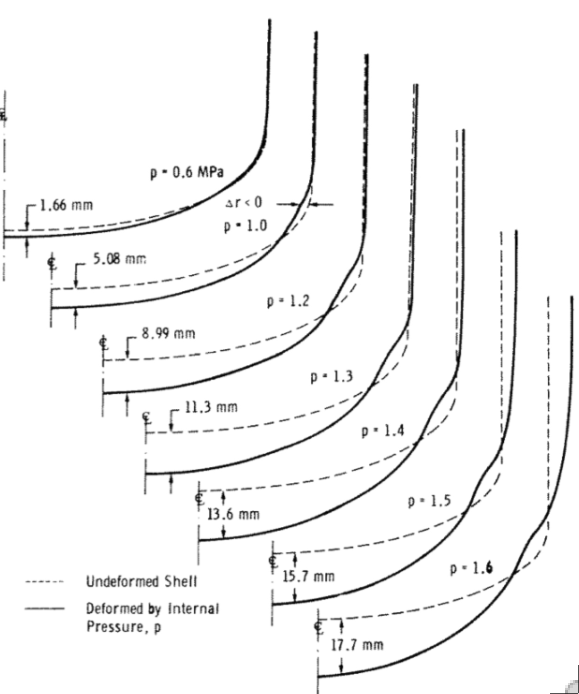
Axisymmetric deformations predicted by BOSOR5 for an internally pressurized ellipsoidal pressure vessel head. Elastic-plastic bifurcation buckling (not shown here) is caused by the relatively narrow band of circumferential compression that occurs in the knuckle region. Accurate predictions of incipient buckling require the inclusion of both nonlinear geometric and material behavior in the simulation.
- Long abstract
- Full paper
- Scope
- Runstream
- Imposed End Shortening
- General Geometry Warning!
- Ellipsoidal Geometry Warning!
- More warnings in letters and notes
- Nonlinear Axisymmetric Collapse Warning!
- More information about the BOSOR5 runstream
BOSOR5 performs axisymmetric collapse and non-axisymmetric bifurcation buckling including elastic-plastic material behavior and creep. It does not supersede BOSOR4, as it has no modal vibration capability or linear non-axisymmetric stress analysis capability.
